Las matemáticas están presentes en nuestra vida en múltiples maneras y una de ellas es en el arte. La relación entre las matemáticas y las artes es evidente en muchos casos. En otros es, cuanto menos, intuible y, a veces, es sencillamente sorprendente. Hoy, 15 de abril, en la División Educativa de CASIO celebramos el Día Mundial del Arte con algunos ejemplos de esa conexión que existe entre las distintas manifestaciones artísticas y las matemáticas.

La geometría y los patrones simétricos
La geometría es una rama de las matemáticas que se ocupa del estudio de las propiedades de las figuras en el plano o el espacio. Es la base teórica del dibujo técnico. Su estudio es muy antiguo y ya la encontramos presente en la civilización babilónica, que fue una de las primeras culturas en incorporar el estudio de la geometría. Cuando se inventó la rueda comenzó la investigación y el estudio de la circunferencia. Tiempo después, ligado a este estudio camina el descubrimiento del número π. Las primeras aproximaciones históricas se las debemos a los primeros matemáticos romanos que descubrieron una relación entre la longitud de pies de la circunferencia y el número 3,14. También hacia el 1900 a.C., en Mesopotamia, hay valores aproximados a Pi y en los documentos matemáticos hallados en la cultura egipcia hay referencias al estudio de los círculos, por ejemplo en el papiro Rhind.

Los patrones simétricos ocurren en la naturaleza y fueron representados artísticamente de muchas maneras. En arquitectura, por ejemplo, encontramos una evidente simetría en las catedrales góticas, en edificios como el Taj Mahal y en la decoración morisca en lugares tan reseñables como la Alhambra, que utilizan patrones complejos con simetrías de traslación y reflexión y también con rotaciones.

El canon de Policleto
Policleto fue un influyente escultor griego, el más importante junto a Fidias, del periodo clásico. El Doríforo es su obra más conocida, se trata del desnudo masculino que representa el «canon» de Policleto. Numerosos escultores, no sólo de Grecia y Roma sino posteriormente en el Renacimiento, tomaron como referencias para sus obras esta indicación.
En este cánon hay un estudio matemático para establecer las proporciones ideales para el escultor, que utilizaba como módulo o medida básica la falangeta del meñique. Policleto multiplicaba esta longitud por la raíz cuadrada de dos (√2) para obtener la distancia de la segunda falange y esta serie geométrica nos daba la medida del brazo primero y del cuerpo completo.
Leonardo da Vinci y el Hombre de Vitruvio
La fecha elegida para este Día Mundial del Arte conmemora el nacimiento de Leonardo Da Vinci, que nació un día como hoy de 1452. Da Vinci encarna como ningún otro pensador o artista al “hombre del Renacimiento”: un humanista que fue al mismo tiempo pintor, ingeniero, músico, arquitecto, anatomista, paleontólogo, botánico, escritor, inventor…
La relación entre matemáticas y arte se hizo muy intensa en el Renacimiento, cuando los artistas se dieron cuenta de que con nociones básicas de la matemática, como la perspectiva o la simetría, podían hacer que las obras fueran más realistas.
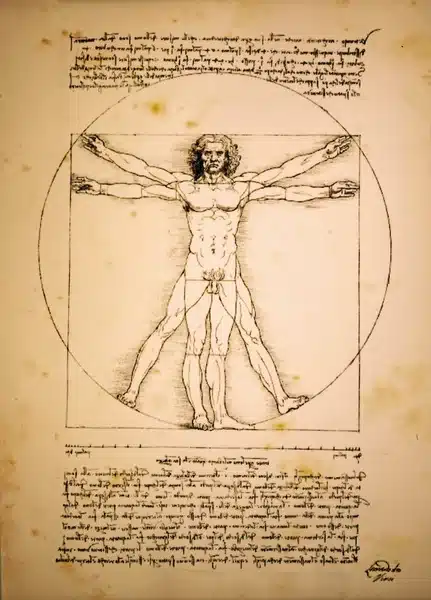
En el caso de Da Vinci os destacamos El Hombre de Vitruvio o Estudio de las proporciones ideales del cuerpo humano. Se trata de un famoso dibujo basado en los textos de Vitruvio, un arquitecto de la antigua Roma. Representa una figura masculina desnuda en 2 posiciones sobreimpresas de brazos y piernas e inscrita en una circunferencia y un cuadrado. Cada parte del cuerpo tiene unas proporciones determinadas: la cabeza mide una octava parte de todo el cuerpo, el pie equivale a un sexto de la altura del hombre, el pecho equivale a una cuarta parte, etc. Otra de las aportaciones de Leonardo da Vinci es la ilustración del libro De divina proportione, escrito por Luca Pacioli, sobre las proporciones matemáticas y su aplicación al arte y la arquitectura.
Fibonacci y el número áureo
La sucesión de Fibonacci, descrita por Leonardo de Pisa, comienza con dos números naturales cualesquiera y a partir de estos, cada término es la suma de los dos anteriores: 0, 1, 1, 2, 3, 5, 8, 13…
El arte se relaciona con la proporción áurea y nuestra percepción de la belleza conecta con esa composición que aparece en la pintura, la arquitectura e incluso en la música.
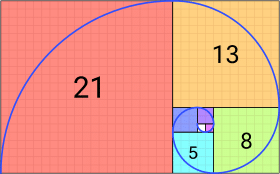
Pero ¿cómo se relaciona la sucesión Fibonacci con el número de oro? Si divides cualquier número en la secuencia de Fibonacci por el anterior, por ejemplo, 233/144, la respuesta siempre es cercana a 1.61803. Ese 1,61803 es lo que se conoce como el número áureo o número phi.
El número áureo está presente en las relaciones entre altura y el ancho de aquéllo que se representa en un cuadro, por ejemplo. También, en arquitectura, en el Partenón de Atenas o en la gran pirámide de Keops, la mayor del mundo.
Cubismo: Pablo Picasso
Cuando mencionamos las formas geométricas y el arte, rápidamente se nos vienen a la cabeza las obras cubistas de Picasso. El pintor malagueño trataba las formas de la naturaleza por medio de figuras geométricas y desde la llamada «perspectiva múltiple» se representaban todas las partes de un objeto en un mismo plano.
Según apuntan algunos autores como Mercedes Siles, catedrática de Álgebra de la Universidad de Málaga que ha indagado en las conexiones del artista con las matemáticas, en la época del surgimiento del cubismo “hay un bullir de ideas, de intercambio de arte y ciencia, y eso cala en Picasso, que quería romper y no ser continuista, no seguir a los maestros, sino hacer su propio camino“.

En el blog Matemolivares se explica de esta forma la esencia del cubismo: “Desde el punto de vista matemático la definición de cubismo podría simplificarse así. De un cubo 3D como máximo podemos ver 3 caras; un ser 4-dimensional podría ver los 6 lados a la vez. El cubismo –Picasso- lo que hizo fue deconstruir el cubo 3D en 6 facetas. Luego pintarlo en 2D y verlo como si estuviéramos en la cuarta dimensión”
La banda de Möbius

La cinta o banda de Möbius es una superficie con una sola cara y un solo borde. Tiene la propiedad matemática de ser un objeto no orientable y ha sido fuente de inspiración en distintos artistas que han recogido esta idea y la han plasmado en sus obras, como el artista británico Richard Fox, el neerlandés M.C. Escher o el escultor japonés Keizo Ushio, cuya obra vemos en la imagen.

También le sirvió a Salvador Dalí para hacer sus grifos de oro macizo de la bañera de la sala de baño de Gala, en el Castillo Gala Dalí, que diseñó a partir de la cinta de Möbius. Podemos ver el detalle en el remate superior del grifo (en la foto de la derecha).
Nos quedamos cortos porque los ejemplos que podríamos poner de las conexiones entre el arte y las matemáticas son muchos. En realidad todos y cada uno de nosotros podemos ver interesantes puntos de confluencia en las distintas obras artísticas que contemplemos. Veamos y sintamos más allá de lo que la impronta del amor a primera vista por un cuadro o un edificio singular nos asalte en un primer momento. Seguro que podemos encontrar, juntas, matemáticas y arte en numerosas ocasiones.












Comments are closed.